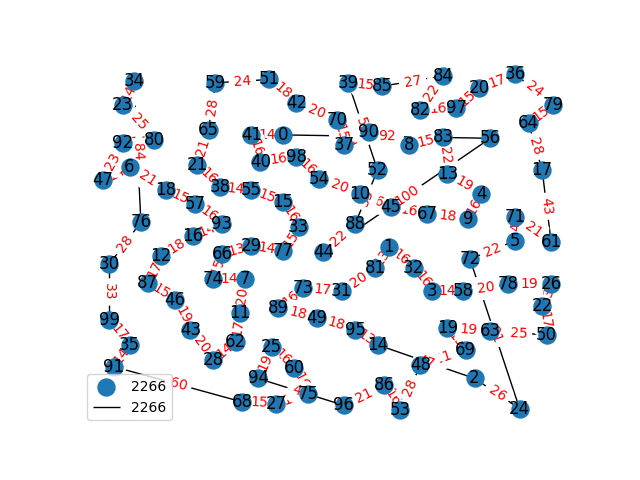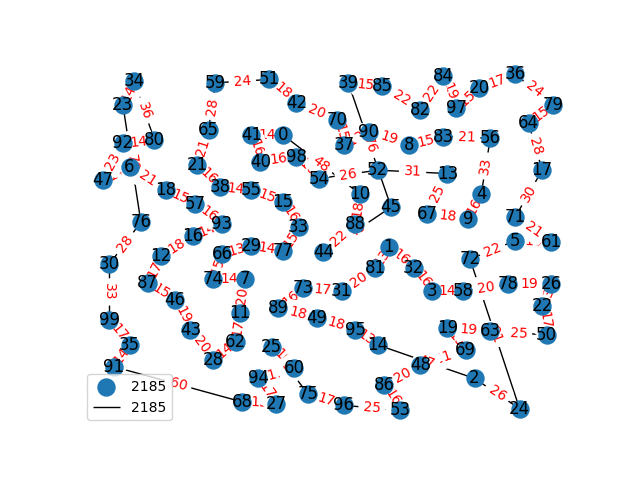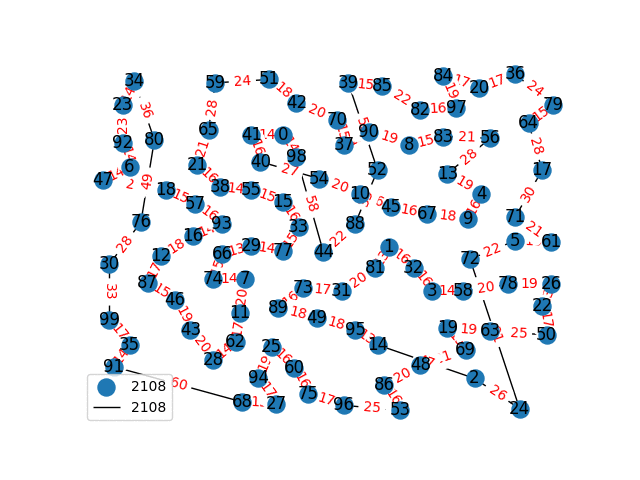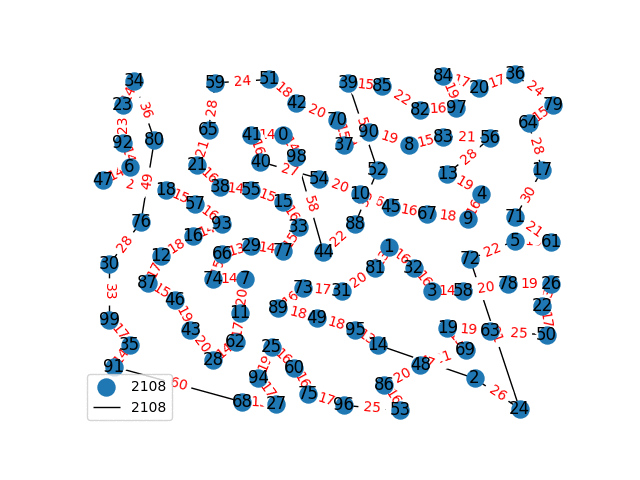
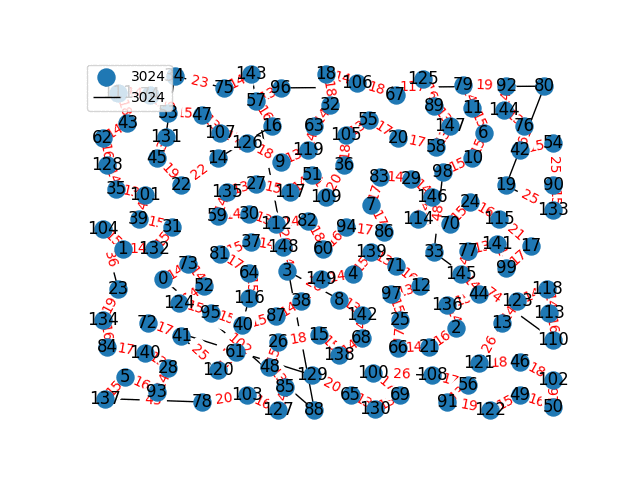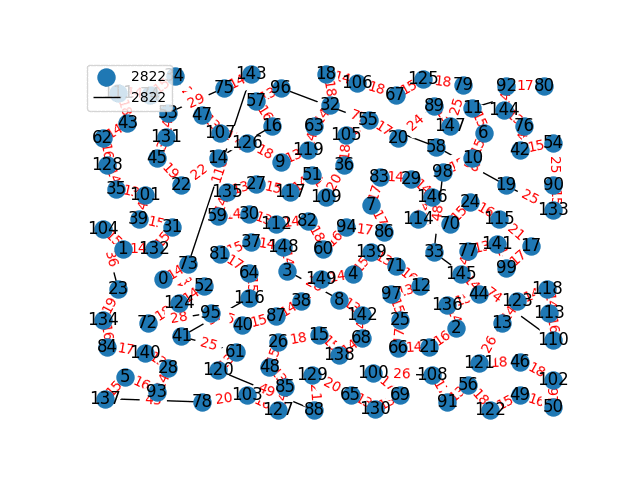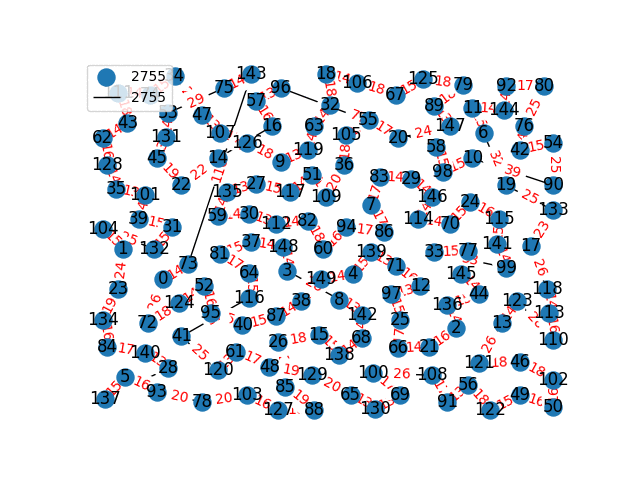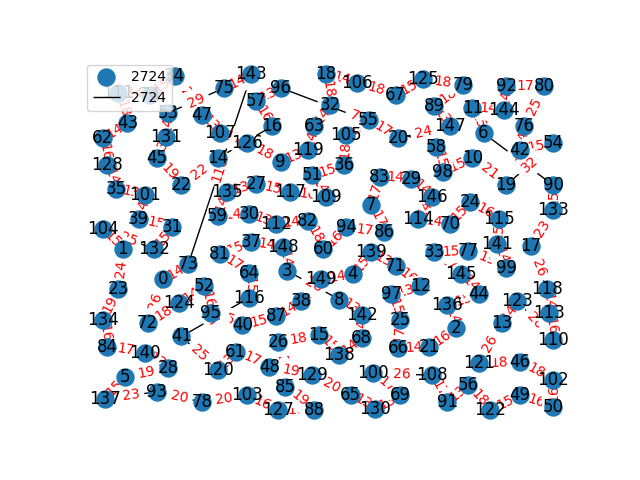
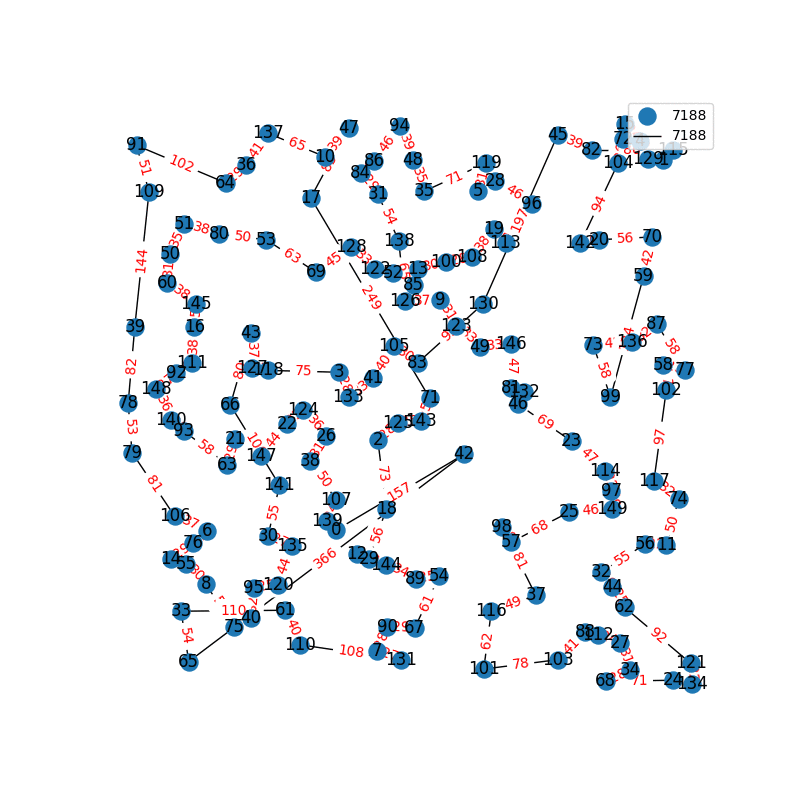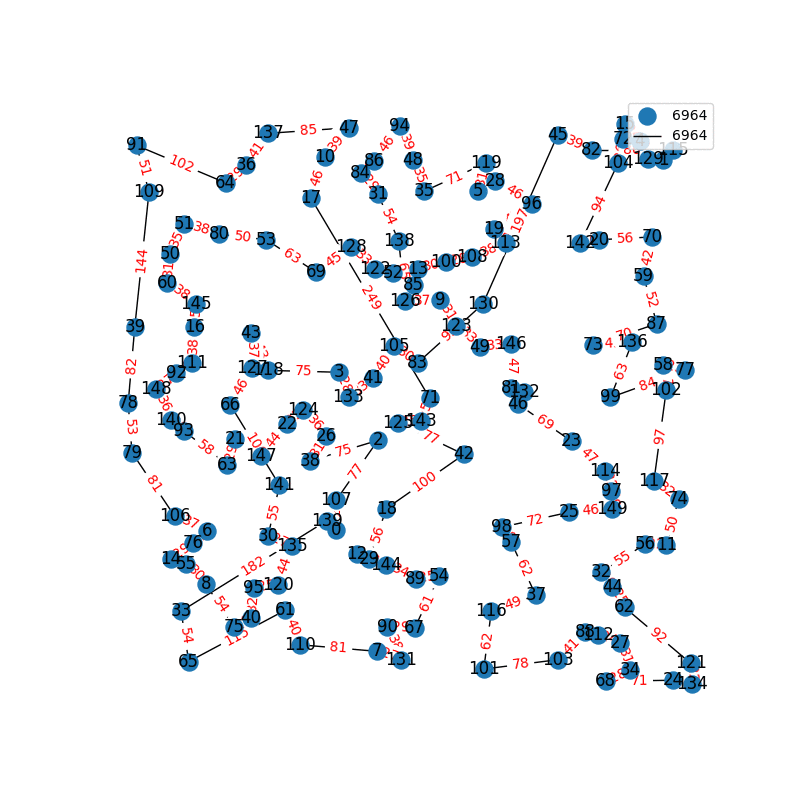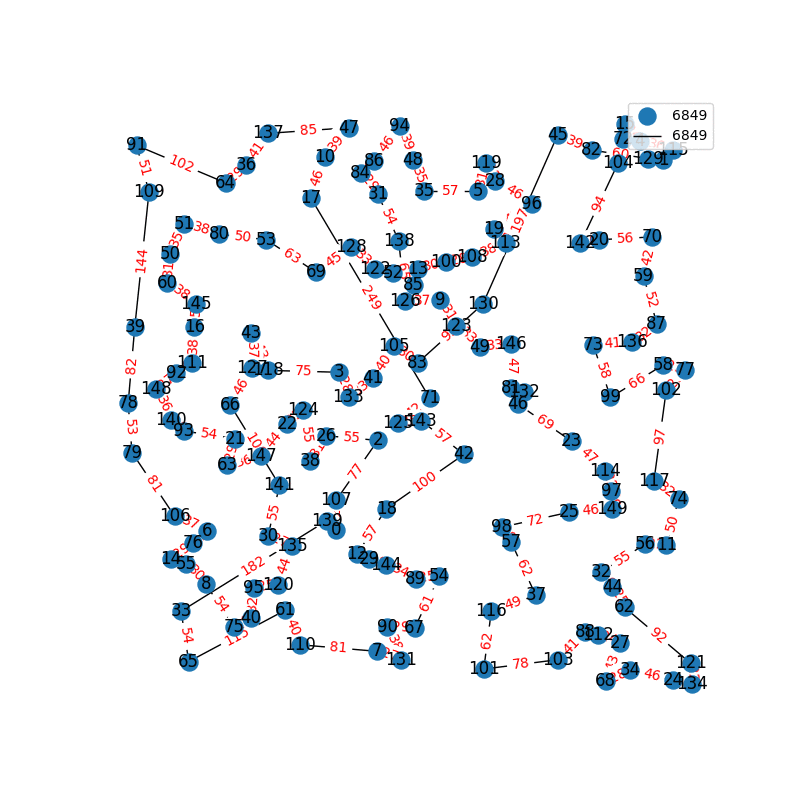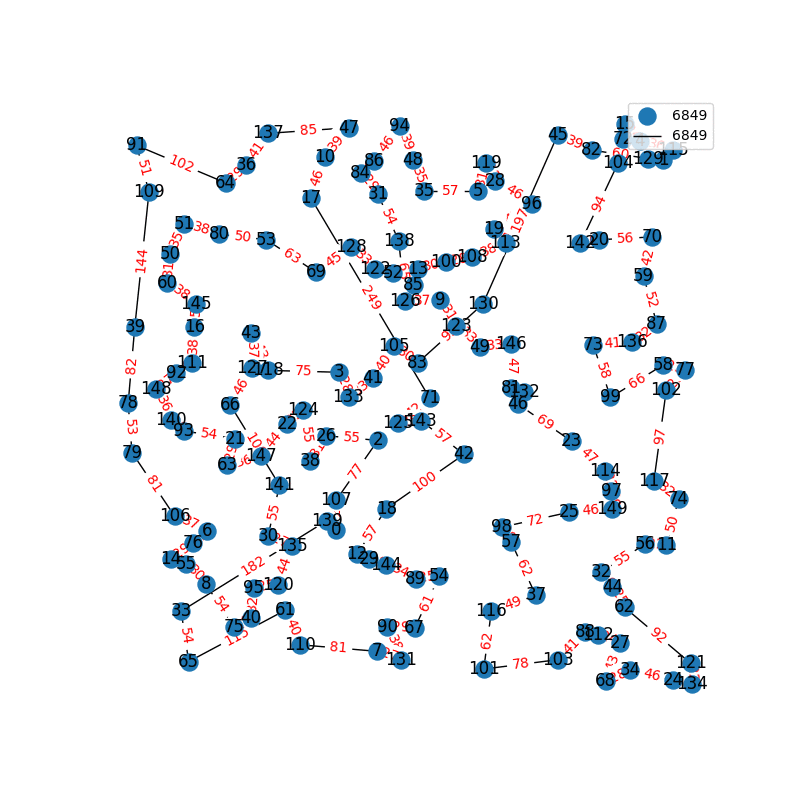
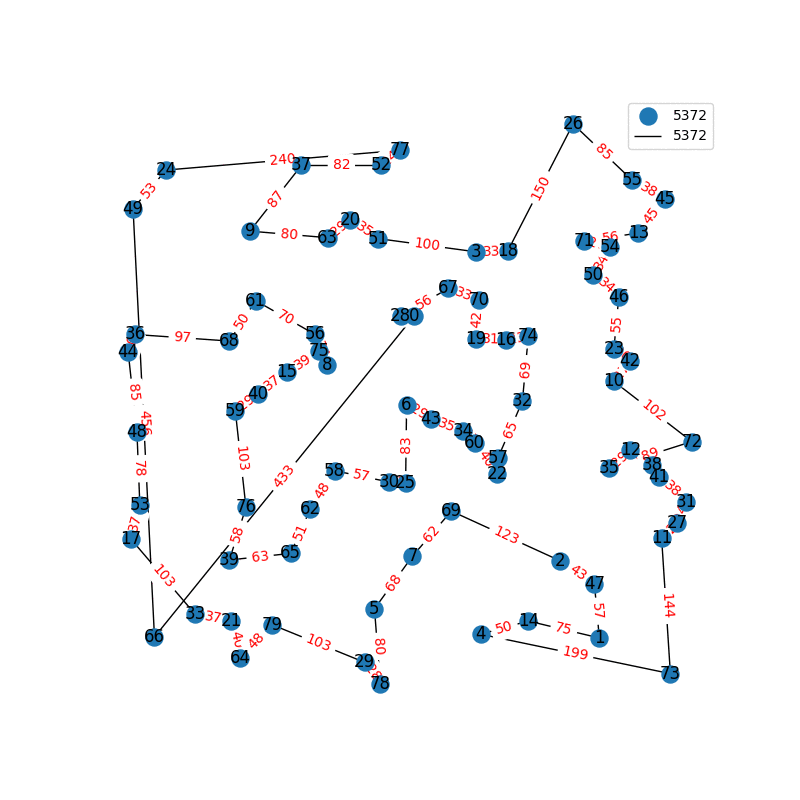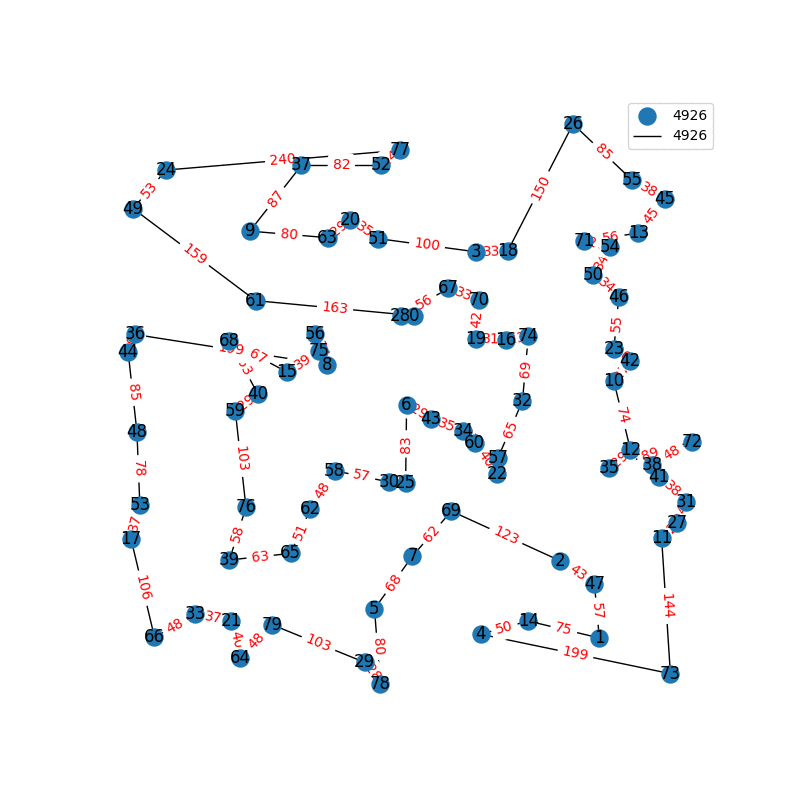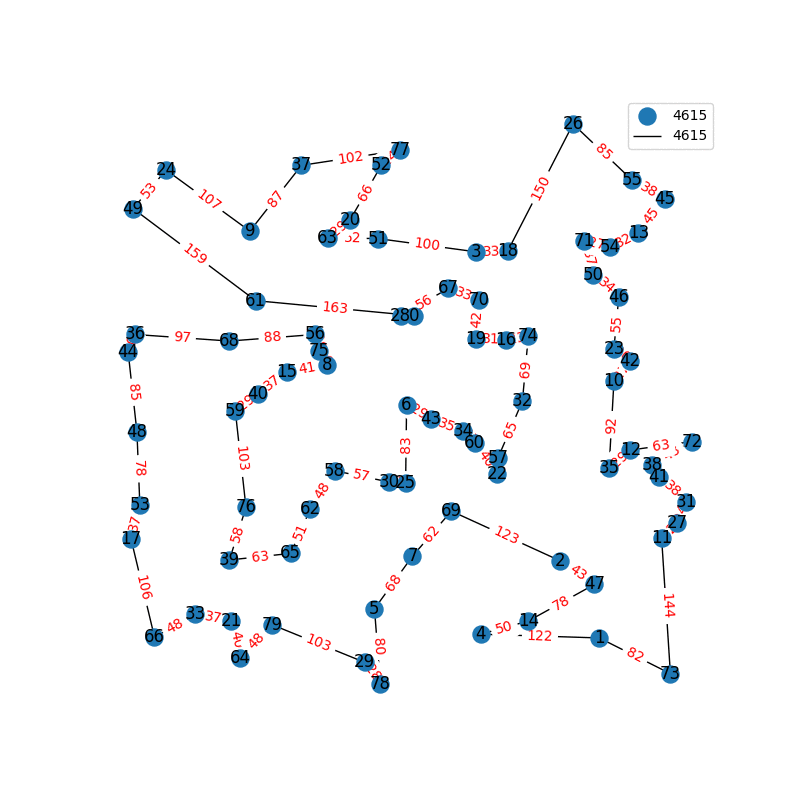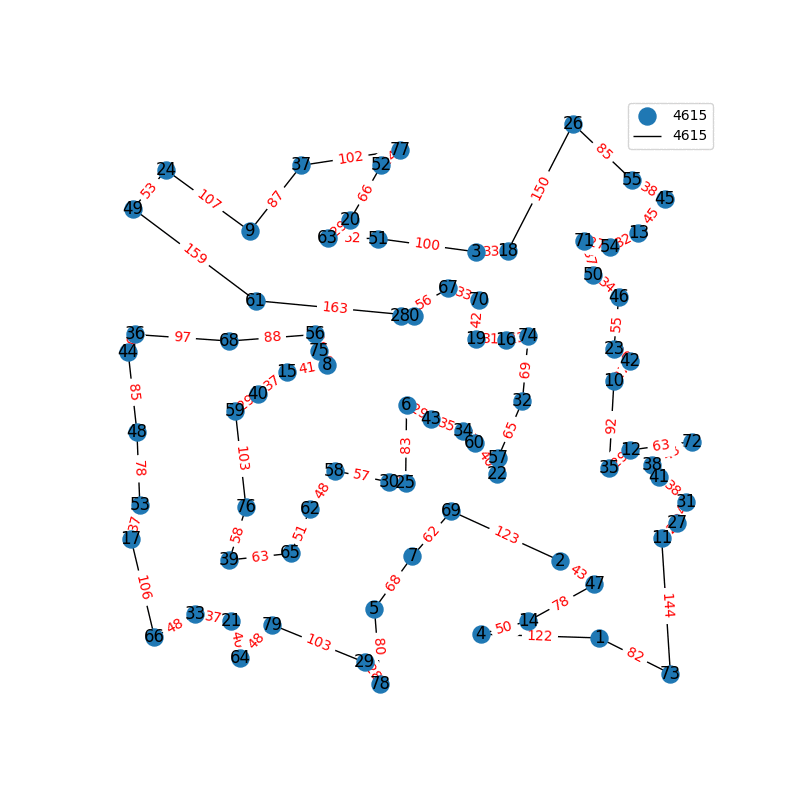
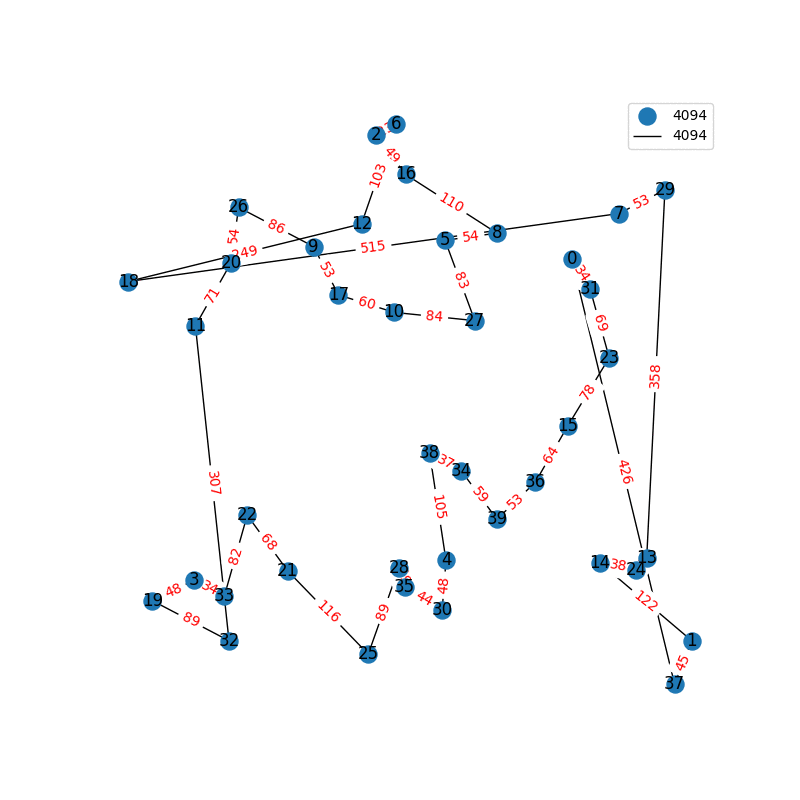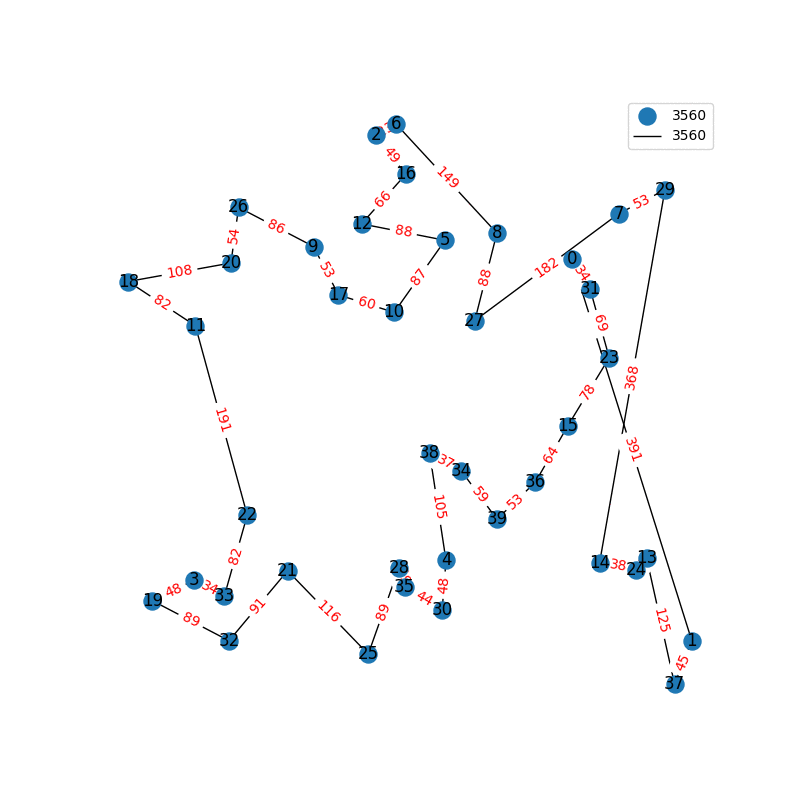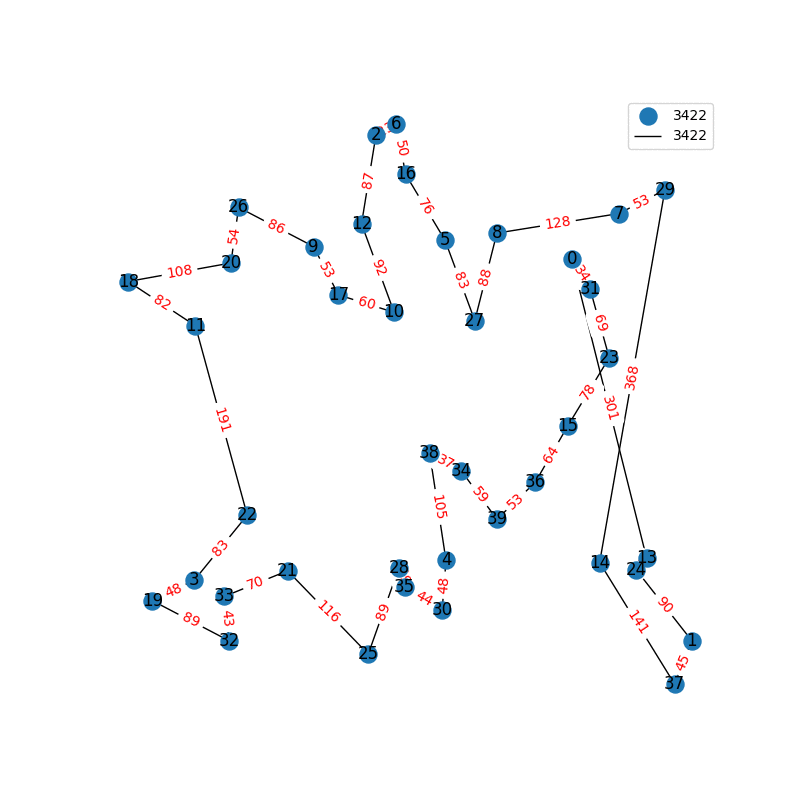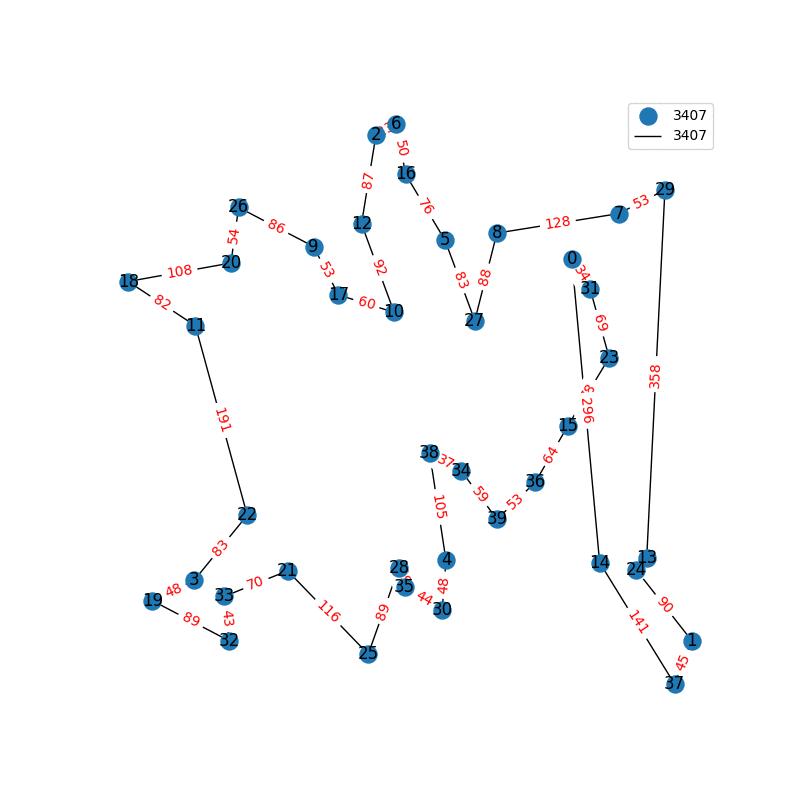
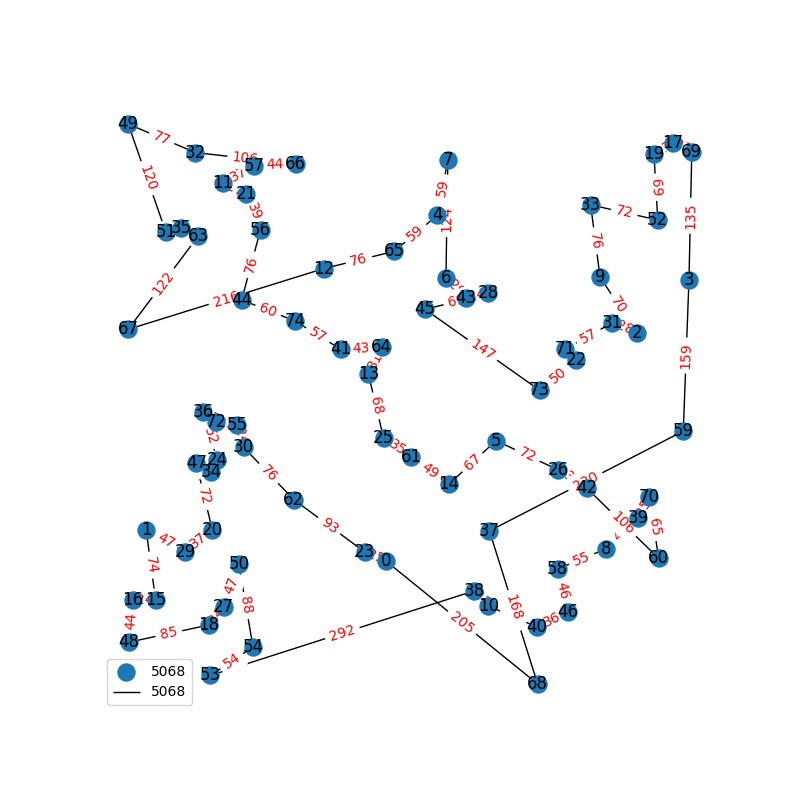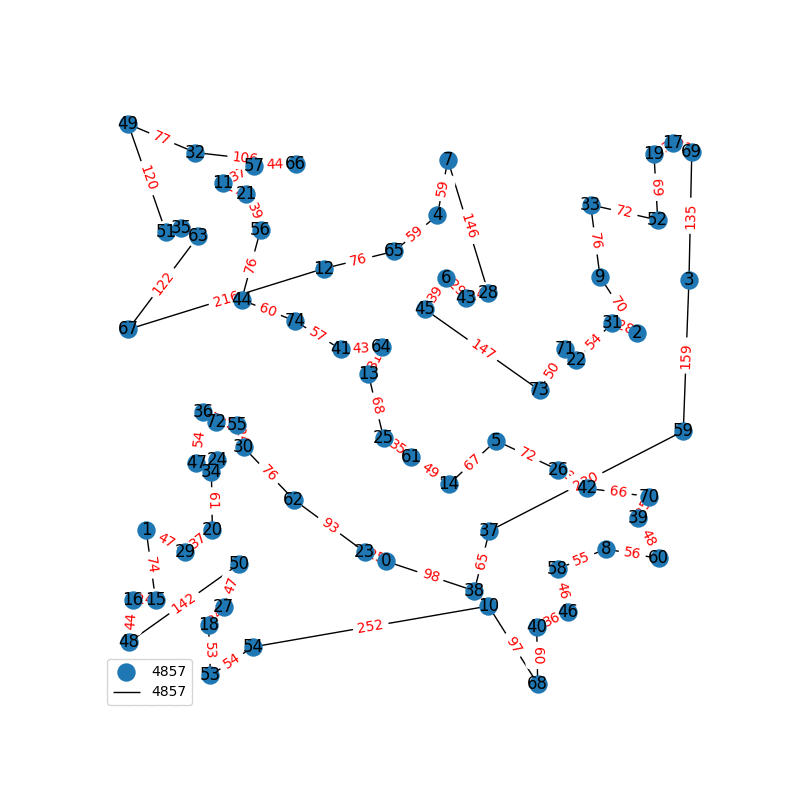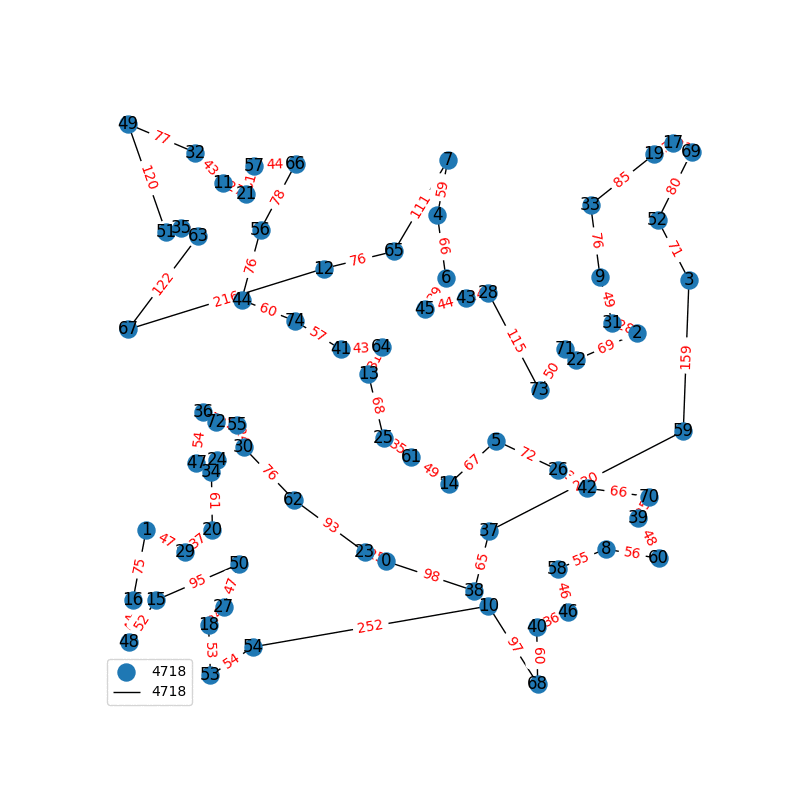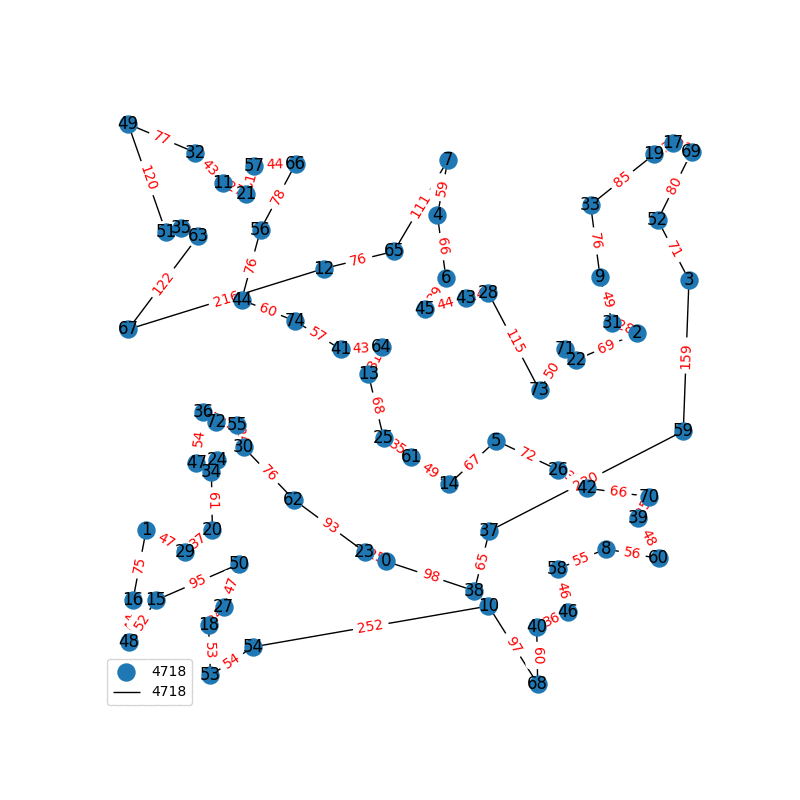
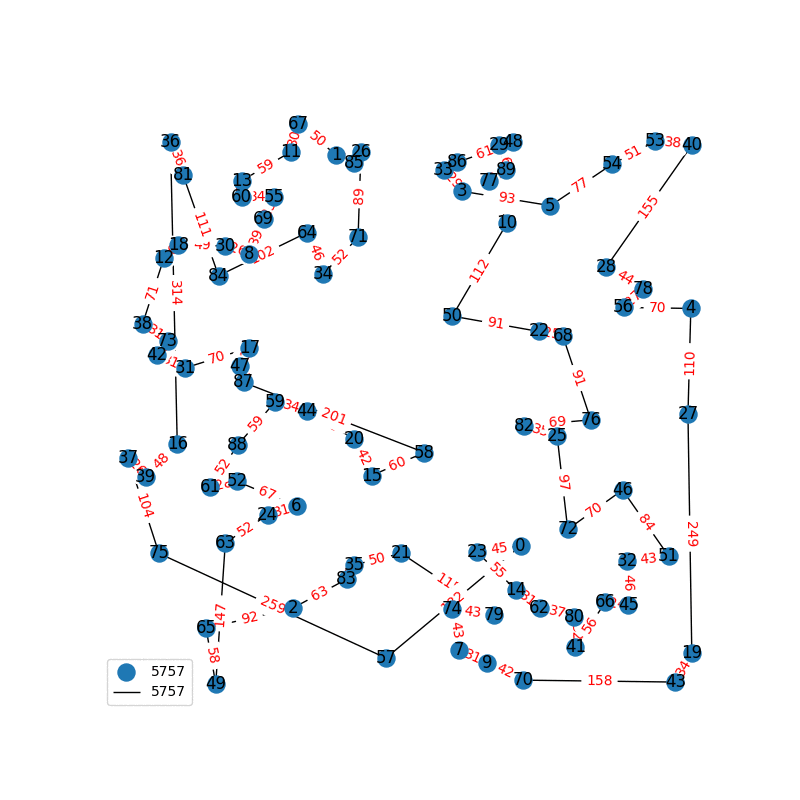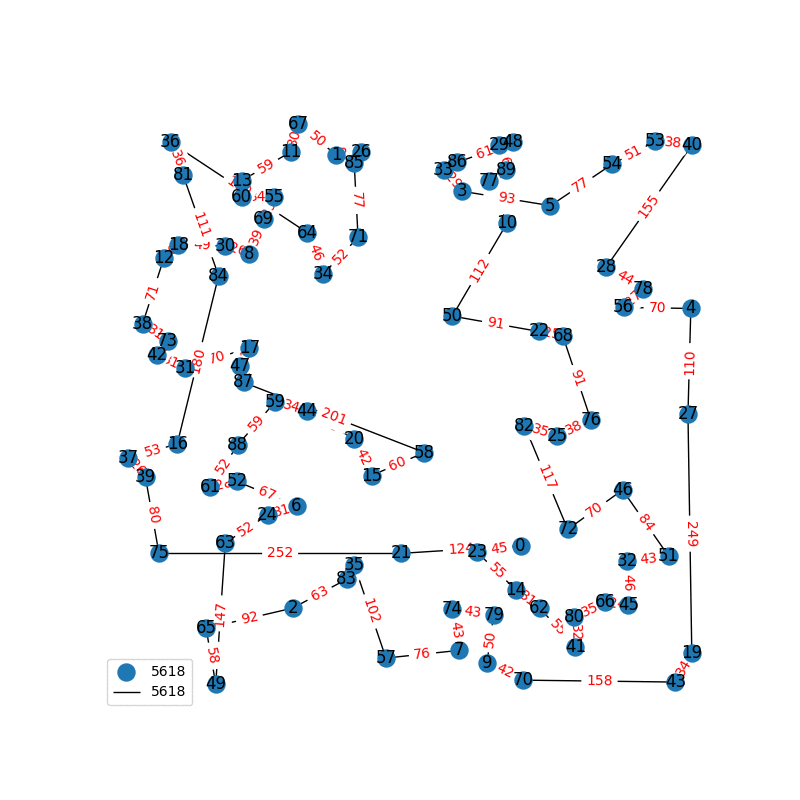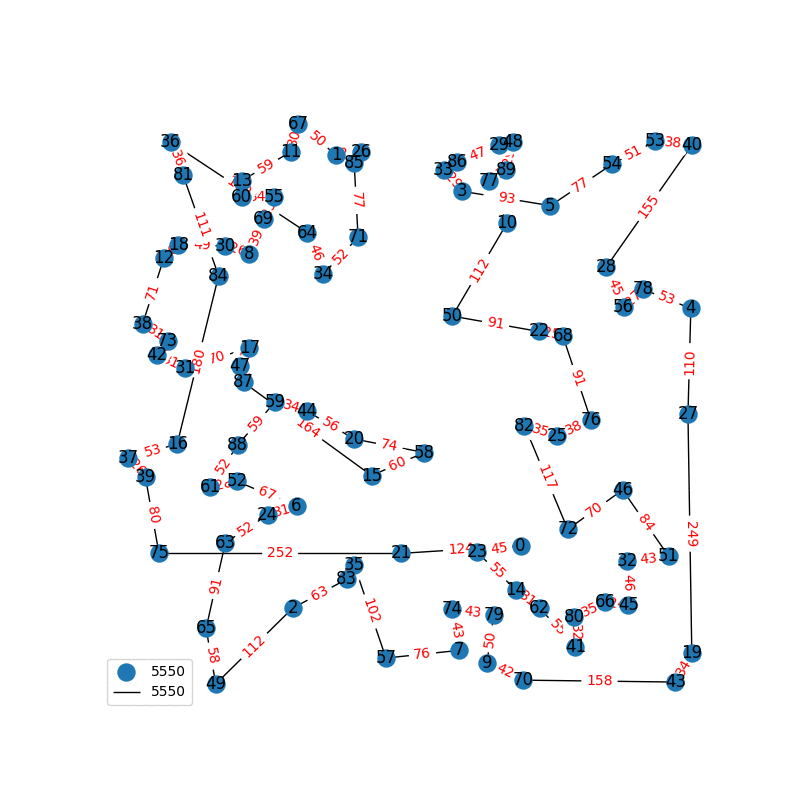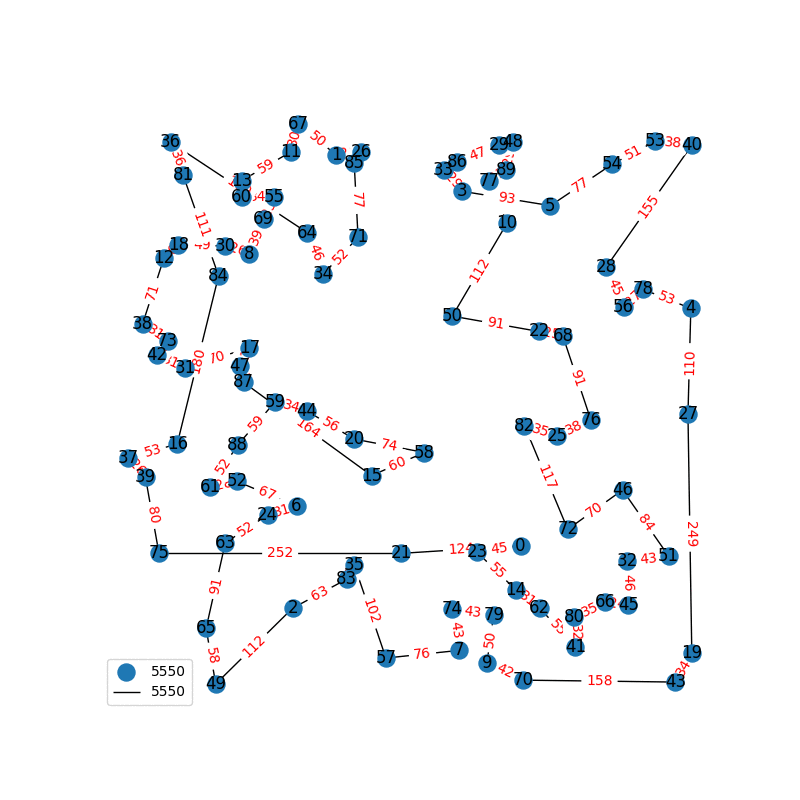
Travelling Salesperson Revisited
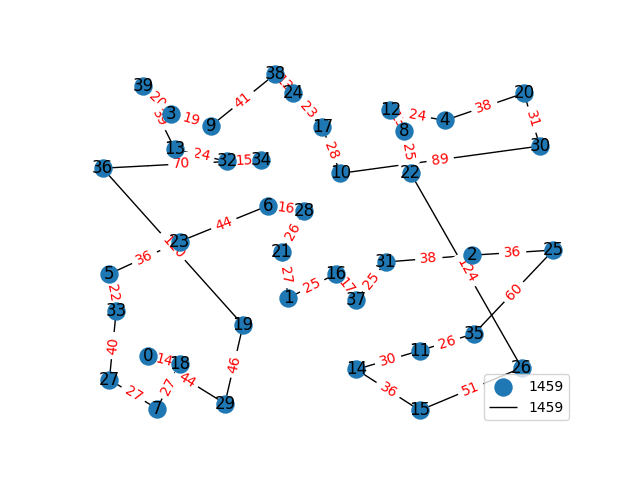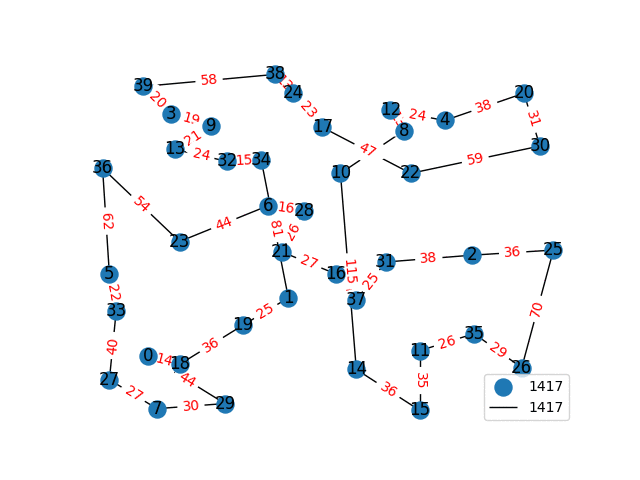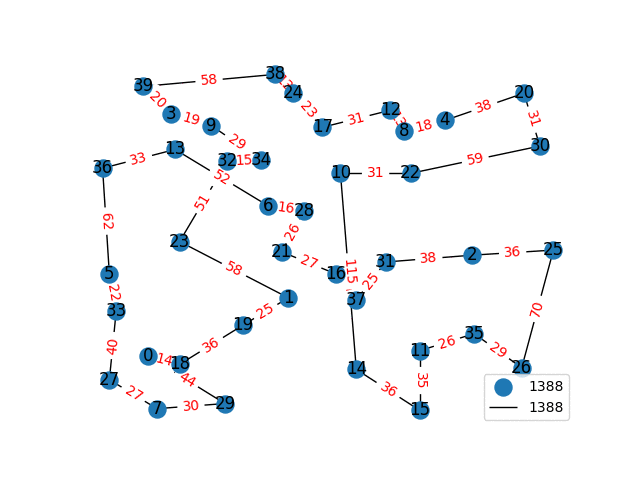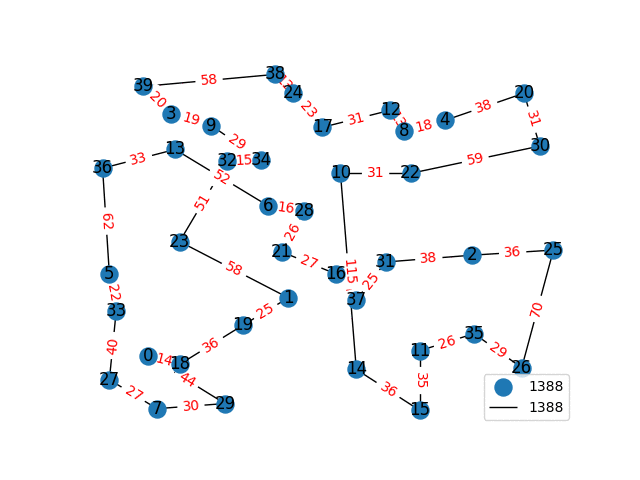
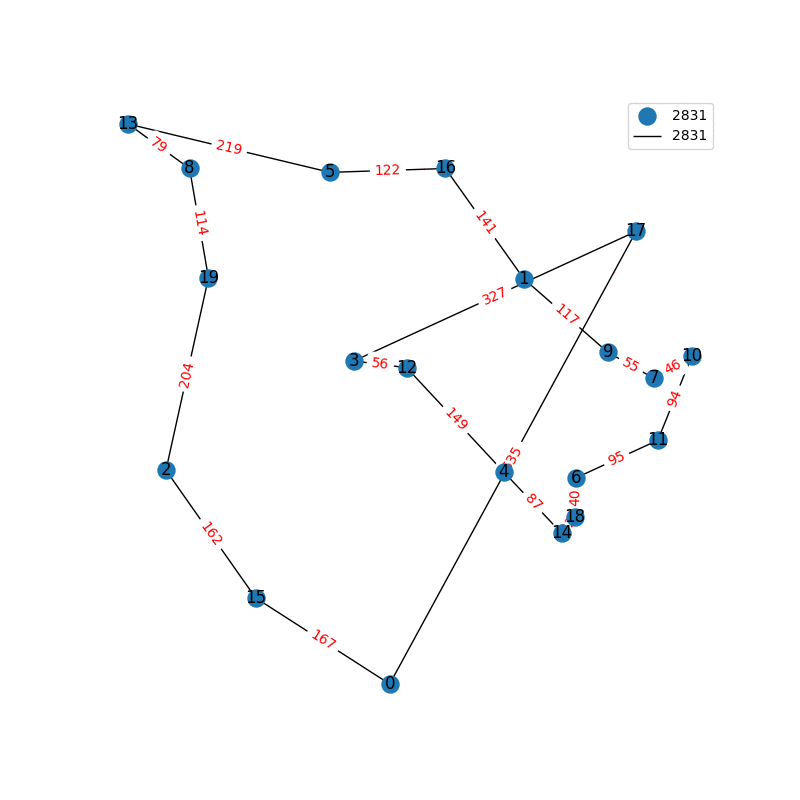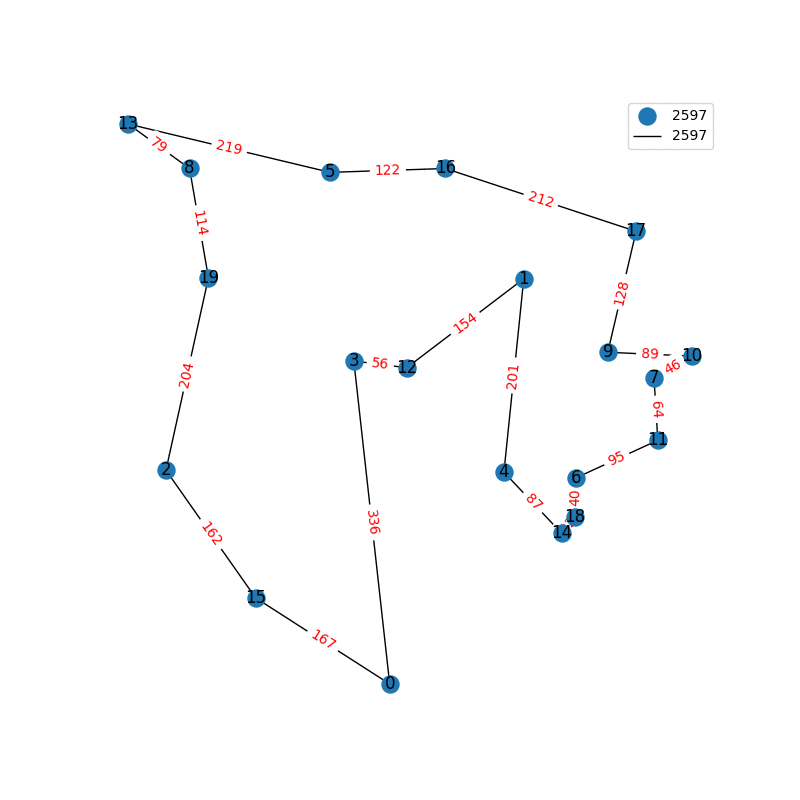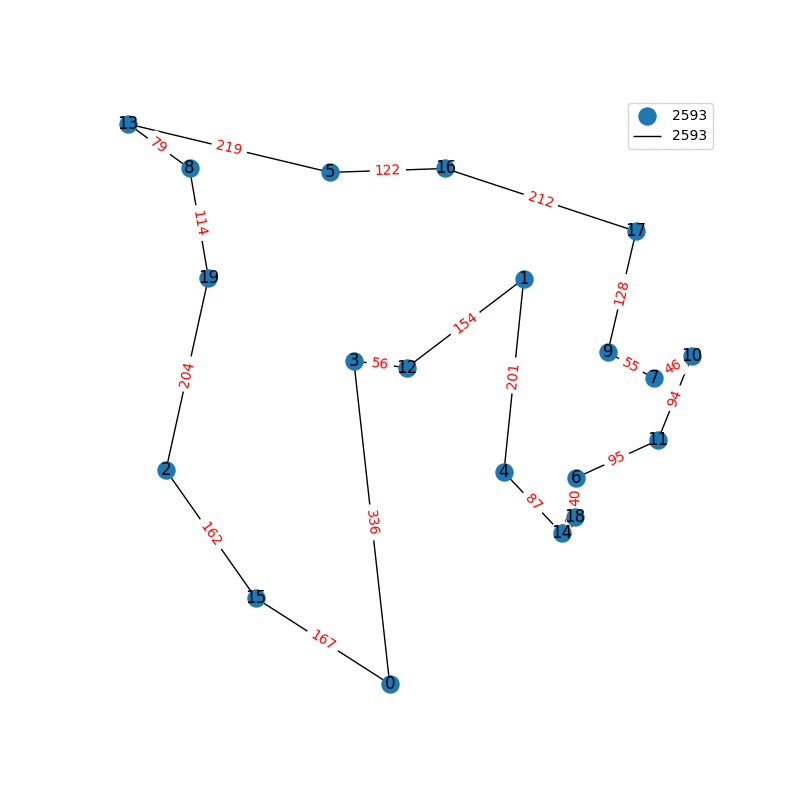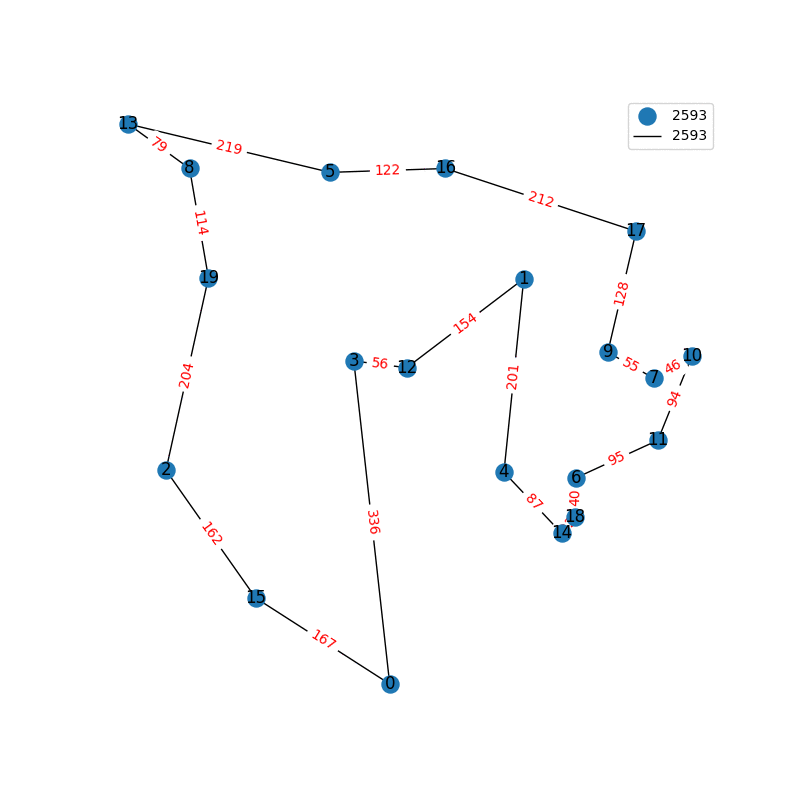
I have decided to come back to the TSP problem. I have optimized my approximation. So first of all, my nearest neighbor was not very good in the previous one. I have fixed it, and now we get really nice graphs to start with. One of the main flaws of what I have is we’re kind of forced to begin in a place for the nearest neighbor(depending where you start it may give you less or better beginning approximation). The other main issue with what I have, is I don’t know if what I have is really any good. It’s sort of a mix mash of heuristics from Wikipedia. I’ll post more some other day, but I have attached the approximations I have been able to create. These were all calculated in under 30 seconds, most of them in the 4-10 second range on a modern i7 2.9 Ghz CPU.
These graphs are incredibly tricky to solve. Technically for a 100 node graph there are, \(9332621544394415268169923885626670049071596826438162146859296389521\\ 7599993229915608941463976156518286253697920827223758251185210916864\\ 00000000000000000000000\) different solutions, that all would need to be checked to guarantee the optimal solution. A 40 node graph, is approximated in just 1-2 seconds on my computer with this heuristic, there are \(815915283247897734345611269596115894272000000000\) different graphs that would need to be checked to find the most optimal solution. This problem is also believed to be NP-Complete, so the best we can do are approximations.