Travelling Salesperson Problem
So the Travelling Salesperson Problem, is a really cool problem in Mathematics and Computer Science. For more information see, Wikipedia and Youtube Visualization.
So I want a solution that would be nice for a handheld phone. It’s a combination of a Greedy Nearest Neighbor search, and Lin-Kernighan Heuristic with a cut off for when we hit the local minimum. I didn’t want to cut it off with some high limit. I wanted it to search until the search became futile compared to some upper limit. I’ve written a small little program(I also made it one file so you can try it yourself), to implement this heuristic.
Psuedocode
def travellingsalesperson():
# we want a connected adjacency matrix graph with all distances
# If you have say a unbridgable gap, like an ocean put +INF
matrix = getdistancematrix
# conduct nearest neighbor search
nnwalk = _nearestneighbor(matrix)
# ge the total distance of the trip
weight = _getweight(nnwalk, matrix)
i = 0
globali = 0
while i < x and globali < globalmax:
i += 1
globali += 1
# copy the walk
walk = nnwalk[:]
# random 3 opt swap
threeoptswap(walk)
# figure out the weight of the new walk
tweight = _getweight(walk, matrix)
# if it's a good walk, it's our new maximum
if weight > tweight:
nnwalk = walk[:]
weight = tweight
# reset i
i = 0
So the other thing is \(i\) and \(x\). I chose these so we can change the depth of the search. This search will continue until, we’ve gone \(x\) searches without an optimization, or we hit our maximum total iterations. This allows us to either restart with a different heuristic instead of nearest neighbor, or just cutoff at our likely local minimum(the best we can get without breaking structure of our walk). The problem with the Travelling Salesperson is its not an easy problem. To find the optimal solution, is \(O(n!)\) time-complexity, and it is unknown if there even exists an algorithm in \(O(2^n)\). Note: This \(O\) is called the time complexity, and it is the asymptotic bound basically, it just means this is how the time to complete the program grows as the problem gets bigger. O(n!) is very large, say the time to solve for 10 cities is 5 seconds, 20 cities is \(20!/10!\) times longer or \(\approx 106298\) years.
I would love to do some more analysis, but more importantly I think playing with the Travelling Salesperson Problem is more important, tsp-single-file.py with the code, and the progression over the course of a 12 node graph and a cutofflimit 400,000 which is computed in less than a second on my computer.
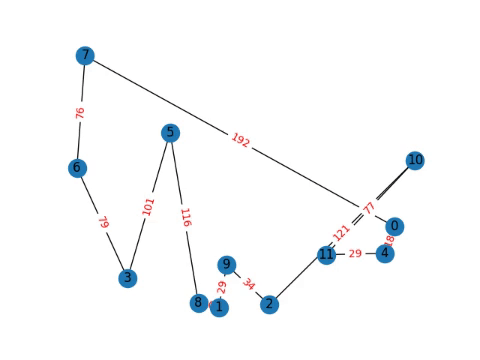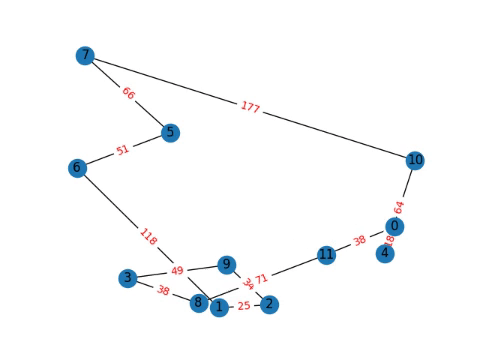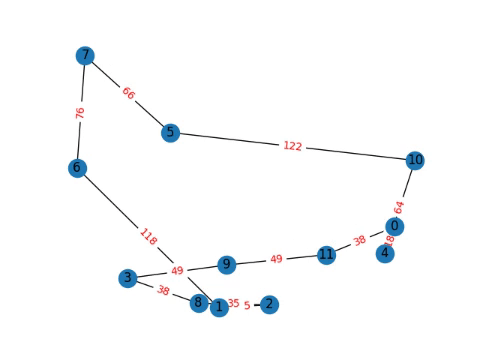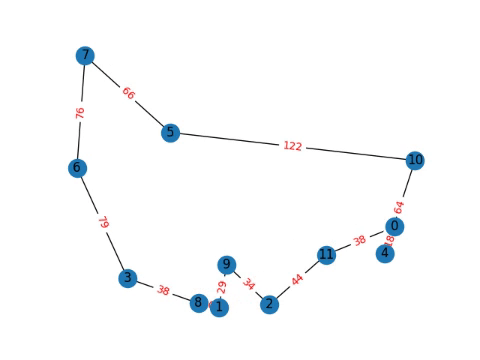
Note:
I know this is not good code, I rewrote all the work I have so I can put it all into one file.
Single File Code to try yourself
# Copyright 2019 Justin Baum
# tsp-single-file.py
# Python3
# Needs networkx(pip3 install networkx)
# Needs plotly(pip3 install plotly)
# To run, (python3 single_fine_tsp.py)
import networkx as nx
import matplotlib.pyplot as plt
import time
import random
count = 1
def showGraph(V, matrix, walk):
global count
X = nx.Graph()
plt.close()
X.add_nodes_from(V.keys())
E =genedges(matrix, walk)
X.add_edges_from(E)
Elabels =genedgelabels(matrix, walk)
nx.draw_networkx_edge_labels(X, V, edge_labels=Elabels, font_color='red', font_size=10)
nx.draw(X, V, with_labels=True)
plt.savefig('fig'+str(count)+'.png')
count += 1
def main():
V = gennodes(12)
matrix = makematrix(V)
nnwalk = _nearestneighbor(matrix)
weight = _getweight(nnwalk, matrix)
showGraph(V, matrix, nnwalk)
i = 0
globali = 0
while i < 400000 and globali < 2000000:
i += 1
globali += 1
walk = nnwalk[:]
threeoptswap(walk)
tweight = _getweight(walk, matrix)
if weight > tweight:
nnwalk = walk[:]
weight = tweight
showGraph(V, matrix, nnwalk)
i = 0
return
## UTILITIES
def gennodes(n, size = 200):
graph = {}
for i in range(n):
x = random.randint(0, size)
y = random.randint(0,size)
graph[i] = (x,y)
return graph
def makematrix(V):
m = len(V)
matrix = [[0 for i in range(m)] for j in range(m)]
for node in V:
for neighbor in V:
point1 = V[node]
point2 = V[neighbor]
matrix[node][neighbor] = int(dist(point1, point2)**0.5)
return matrix
def genedgelabels(matrix, walk):
prev = 0
edges = {}
for step in walk:
edges[(prev, step)] = matrix[prev][step]
prev = step
edges[(prev, 0)] = matrix[prev][0]
return edges
def genedges(matrix, walk):
prev = 0
edges = []
for step in walk:
edges.append([prev, step])
prev = step
edges.append([prev, 0])
return edges
def dist(point1, point2):
return (point1[0] - point2[0])**2 + (point1[1] - point2[1])**2
def threeoptswap(walk):
x = random.randint(0, len(walk)-1)
y = random.randint(0, len(walk)-1)
z = random.randint(0, len(walk)-1)
temp = walk[x]
walk[x] = walk[y]
walk[y] = walk[z]
walk[z] = temp
return
def _nearestneighbor(matrix):
m = len(matrix)
for row in matrix:
assert(m == len(row))
prev = 0
walk = []
unvisited = list(range(m))[1:]
while len(unvisited) > 0:
min = float("inf")
curr = 0
for leg in unvisited:
leglength = matrix[prev][leg]
if leglength < min:
min = leglength
curr = leg
walk.append(curr)
unvisited.remove(curr)
return walk
def _getweight(walk, matrix):
prev = 0
weight = 0
for dest in walk:
weight += matrix[prev][dest]
prev = dest
weight += matrix[prev][0]
return weight
if __name__ == "__main__":
main()